Understanding Artificial Neural Networks

Introduction

Artificial Intelligence (AI) is all the hype these days, every other day OpenAI, Google, or Meta is making headlines with a breakthrough in the field. Every other day we get a paper with a new state of the art method for doing something. When writing this Meta recently came out with its new LLM architecture Large Concept Models (LCMs).

Why isn’t this blog about LCMs? Understanding these breakthroughs is not an easy task and as you know “Rome wasn’t built in a day”. These concepts require you to have basic understanding of machine learning and deep learning, we cannot just jump onto stuff like LLMs, Transformers, CNNs, etc.

Artificial Neural Networks (ANNs) help us build this foundational knowledge in deep learning to move to advanced topics. As a matter of fact, convolutional neural networks (CNNs) which are prominently used to recognize objects in images are a special type of neural networks.

This blog will focus on how ANNs work at core and we’ll also build a neural network from scratch and a scalar auto-gradient library without using any library of any sorts to which will shed a little light on the foundations of deep learning.

---

What are neural networks?

Artificial Neural Networks (ANNs) are known by several names such as multilayer perceptrons, deep feedforward networks, feedforward neural networks, or just neural networks. ANNs comes under the category of Supervised Learning where a mapping from \(x \to y\) is provided to the algorithm and from there it learns complex relationships between independent and dependent variables. This mapping which we provide to the neural network is called the training data.

The goal of neural networks is to approximate some function \(f^*\) so that we can predict the value of a given set of inputs based on the data provided during the training. Neural networks just like other learning algorithms like linear regression or SVM are just a mathematical function.

\[y = f_{NN}(x)\]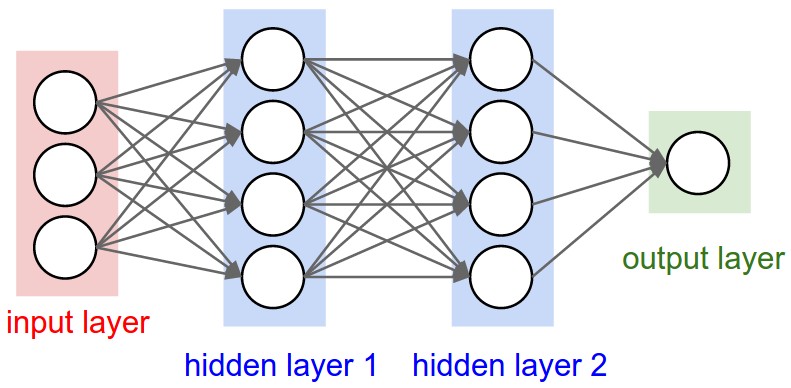

Neural Networks are structures made up of layers of neurons laid out sequentially. The function \(f_{NN}\) has a particular form: it’s a nested function. Each layer of NN can be thought of as one level of nesting in the \(f_{NN}\) function. The structure of neural networks allows the algorithm to learn complex decision boundaries which is not possible in algorithms like linear Regression, logistic regression, etc.

\[y = f_{NN} = f_3(f_2(f_1(x)))\]

Neural networks also eliminate the need for doing steps like feature engineering as the structure is not just a single function but a combination of different functions which are able to evaluate many combinations of data.

There is a misconception that ANNs try to mimic the human brain or the way it works which is wrong, a better statement would be that ANNs are inspired by the structure of the brain. We don’t have enough information on how brains work or function to model it mathematically.

---

Neurons

A neuron is the smallest unit in the neural network, these are the building blocks of neural networks. It can be thought of as a simple mathematical function where inputs are provided and output is received. Every neuron has an activation function which is applied to the input data to get an output. Multiple neurons combine to create a layer of neural network and multiple layers then combine to create the entire neural network.

The image shown above is an example of a neuron, as you can see a neuron body is provided with multiple inputs \((x_i)\), and every input is given a weight \((w_i)\). Along with these inputs, there is also a variable bias \((b)\), an activation function is applied to these inputs to get an output.

\[f(x, w, b) = x_1w_1 + x_2w_2 + \cdots + x_iw_i + b\]

---

Activation Functions

Activation functions play a crucial role in neural networks by introducing non-linearity, allowing the network to learn complex patterns. Without activation functions, a neural network would behave like a simple linear model, limiting its ability to solve real-world problems.

1. Sigmoid Activation Function

The sigmoid function maps any input value to a range between 0 and 1. It is commonly used in binary classification problems.

\[\sigma(x) = \frac{1}{1 + e^{-x}}\]

Properties:

• Output range: (0,1)
• Differentiable, smooth curve
• Causes vanishing gradient problem for very large or very small inputs

2. ReLU (Rectified Linear Unit)

ReLU is one of the most popular activation functions in deep learning. It allows positive values to pass through while converting negative values to zero.

\[ReLU(x) = \max(0, x)\]

Properties:

• Output range: [0, ∞)
• Fast computation
• Helps in reducing vanishing gradient issue
• Can cause dying ReLU problem where neurons get stuck at 0

3. Leaky ReLU

Leaky ReLU improves upon ReLU by allowing small negative values instead of setting them to zero, preventing neurons from dying.

\[LeakyReLU(x) = \max(\alpha x, x)\]

Where \(\alpha\) is a small positive constant (e.g., 0.01).

Properties:

• Output range: (-∞, ∞)
• Prevents dead neurons problem

4. Tanh (Hyperbolic Tangent)

Tanh is similar to sigmoid but outputs values between -1 and 1, making it zero-centered, which can help in training.

\[tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

Properties:

• Output range: (-1,1)
• Zero-centered, better than sigmoid
• Still suffers from vanishing gradient problem

5. Softmax Activation

The softmax function is used in the output layer for multi-class classification problems. It converts raw scores into probabilities.

\[softmax(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}\]

Properties:

• Converts outputs into probability distribution
• Used in classification tasks where multiple classes are involved

Choosing the Right Activation Function

• Hidden Layers: Use ReLU or Leaky ReLU for deep networks.
• Output Layer:
  • Use Sigmoid for binary classification.
  • Use Softmax for multi-class classification.
  • Use Tanh when outputs need to be zero-centered.

Activation functions are a key part of how neural networks learn. The right choice depends on the problem being solved and the depth of the network.

---

Layers and Architectures

Now that we understand neurons, let’s see how they come together to form a neural network. A neural network is made up of layers of neurons, where each layer processes information and passes it forward.

Types of Layers

1. Input Layer:

This is the first layer of the network that takes in the raw data. Each neuron in this layer represents a feature from the dataset.

2. Hidden Layers:

These are the layers between the input and output layers. They perform most of the computations and learn complex patterns. A neural network with multiple hidden layers is called a deep neural network.

3. Output Layer:

The last layer of the network gives the final prediction. The number of neurons here depends on the type of problem.

• For regression, there’s usually one neuron giving a continuous output.
• For classification, the number of neurons matches the number of classes.

Architecture of a Neural Network

The structure of a neural network is determined by:

• Number of layers: More layers mean the network can learn more complex patterns.
• Number of neurons per layer: More neurons can capture more details but may lead to overfitting.
• Connections between layers: Most networks are fully connected, meaning each neuron in one layer connects to every neuron in the next layer.

Choosing the Right Architecture

Designing a neural network isn’t just about adding more layers and neurons. Too many can lead to overfitting, while too few might not capture enough patterns. The best approach is to experiment and fine-tune based on the problem.

The architecture of a network depends on the task:

• Feedforward Neural Networks (FNNs): Used for general-purpose tasks.
• Convolutional Neural Networks (CNNs): Best for image-related tasks.
• Recurrent Neural Networks (RNNs): Used for sequential data like text and time series.

Each of these architectures has its strengths, and choosing the right one depends on the problem at hand.

---

Forward Propagation

Now that we know how neural networks are structured, let’s see how they actually make predictions. The process of passing inputs through the network to get an output is called forward propagation. Step-by-Step Process for it is the following:

1. Take Inputs

The input layer receives the raw data and passes it to the next layer. Each neuron in this layer represents a feature from the dataset.

2. Apply Weights and Biases

Each connection between neurons has a weight that determines how important an input is. Each neuron also has a bias to adjust the output.

The neuron calculates the weighted sum of inputs plus the bias:

\[z = x_1w_1 + x_2w_2 + \dots + x_nw_n + b\]

3. Apply Activation Function

The weighted sum is then passed through an activation function, which introduces non-linearity and helps the network learn complex patterns:

\[a = f(z)\]

4. Pass to the Next Layer

The output of each neuron becomes the input for the next layer, repeating the same process until the output layer is reached.

5. Generate Final Output

The last layer produces the final prediction. If it’s a classification task, this could be a probability score. If it’s regression, it could be a continuous value.

Why Forward Propagation?

Forward propagation is the foundation of neural networks. It helps the network process data step by step, layer by layer, to make predictions. However, just passing data forward isn’t enough—neural networks also learn by adjusting their weights. That’s where backpropagation comes in, which we’ll discuss next.

---

Loss Functions and Backpropagation

Now that we understand forward propagation, we need to answer a crucial question: How does a neural network learn?

When we first initialize a neural network, the weights and biases are set randomly, meaning the predictions it makes will be completely off. Our goal is to adjust the weights and biases so that the network makes accurate predictions. This is done using two key concepts:

1. Loss Functions – Measure how far the predictions are from the actual values.
2. Backpropagation – Adjusts the weights and biases to reduce the loss and improve accuracy.

Let’s go step by step.

---

Loss Functions: Measuring Error

A neural network learns by minimizing error, and to measure this error, we use a loss function.

A loss function compares the network’s predicted output \(y_{\text{pred}}\) with the actual output \(y_{\text{true}}\) and gives a numerical value indicating how bad the prediction was. The goal is to make this number as small as possible.

Common Loss Functions

Depending on the type of problem, different loss functions are used:

1. Mean Squared Error (MSE) – For Regression Problems

Used when predicting continuous values. It calculates the squared difference between the actual and predicted values:

\[L = \frac{1}{n} \sum (y_{\text{true}} - y_{\text{pred}})^2\]

• Large errors contribute more due to squaring.
• Encourages smaller differences between predicted and actual values.

2. Cross-Entropy Loss – For Classification Problems

Used when predicting categories (e.g., cat vs. dog). If we have multiple classes, cross-entropy loss is used to measure how different the predicted probability distribution is from the actual labels:

\[L = -\sum y_{\text{true}} \log(y_{\text{pred}})\]

• Punishes incorrect confident predictions heavily.
• Encourages the model to assign high probabilities to the correct class.

Why is Loss Important?

The loss function tells us how good or bad our neural network is. But knowing this isn’t enough—we also need a way to improve the network. That’s where backpropagation comes in.

---

Backpropagation: How Neural Networks Learn

Backpropagation is the heart of training a neural network. It’s the process of adjusting weights and biases to reduce the loss, making the network better over time.

The Core Idea

Backpropagation works by moving backward through the network and tweaking the weights in the direction that reduces the loss. It uses an optimization algorithm called gradient descent, which we’ll discuss shortly.

Step-by-Step Explanation

1. Compute the Loss

First, we calculate the loss using a loss function (MSE or cross-entropy).

2. Calculate Gradients (Derivatives)

The loss depends on the weights and biases. Backpropagation computes how much each weight and bias contributed to the loss using partial derivatives.

Mathematically, we find:

\[\frac{\partial L}{\partial w}\]

This tells us:

• If \(\frac{\partial L}{\partial w}\) is positive, decreasing \(w\) will reduce loss.
• If \(\frac{\partial L}{\partial w}\) is negative, increasing \(w\) will reduce loss.

3. Update Weights Using Gradient Descent

We adjust each weight using gradient descent, which updates weights in the opposite direction of the gradient:

\[w_{\text{new}} = w_{\text{old}} - \eta \cdot \frac{\partial L}{\partial w}\]

• \(\eta\) is the learning rate, controlling how big the step is.
• A small learning rate makes learning slow.
• A large learning rate can cause instability.

4. Repeat Until Convergence

• We perform this update for all weights and biases.
• The process repeats for multiple iterations (epochs) until the loss is small.

Understanding Gradient Descent

Gradient descent is how backpropagation adjusts weights to reduce the loss. It finds the lowest point on the loss surface, like rolling a ball downhill.

Types of Gradient Descent

1. Batch Gradient Descent

• Uses all training data to compute gradients.
• More stable but slower.

2. Stochastic Gradient Descent (SGD)

• Updates weights after each training example.
• Faster but noisier updates.

3. Mini-Batch Gradient Descent

• Uses small batches of data for updates.
• Balances speed and stability.

Why Does Backpropagation Work?

Backpropagation is based on the chain rule of calculus. Since a neural network is just a nested function, we compute derivatives layer by layer:

\[\frac{\partial L}{\partial w} = \frac{\partial L}{\partial a} \times \frac{\partial a}{\partial z} \times \frac{\partial z}{\partial w}\]

Each layer gets its error gradually corrected by passing gradients backward, ensuring earlier layers learn the right representations.

---

Summary: The Learning Cycle

1. Forward Propagation: Inputs pass through the network to generate predictions.

2. Compute Loss: Compare predictions to actual values.

3. Backpropagation: Compute gradients of loss w.r.t. weights.

4. Gradient Descent:Adjust weights to minimize loss.

5. Repeat: Continue until loss is small.

This is how neural networks learn—by continuously refining their weights using loss functions and backpropagation.